Library of Unloved Models Vol. 2
- Dipyaman Sanyal

- Jun 25, 2024
- 5 min read
Linear regression models are the go-to first step for most of us when we are trying to predict or understand a numerical variable. However, most of us also realize after learning the basics that there are certain limitations of the model. One of the first problems in linear regression models I thought of (and I am sure many others did too) was that the relationships between the Y and the Xs do not change for different levels or values of X or Y. For example, if height is related to age in the data of school going kids, in a linear regression model the relationship between height and age (β) remains constant for all values of age and height. If you look at it from a statistical standpoint if the relationship between X and Y (i.e. the β) changes with the value of X, then it is often a sign of heteroscedasticity (variance of Y increasing with value of X) and thus violates the basic assumptions of a linear regression model.
However, we do know that the linear relationship between X and Y does not remain constant over different values of X and Y. Advertising and marketing professionals will relate to this immediately. Spending the first 100,000 on Facebook ads may yield a very low level of incremental revenues because there was not a critical mass of ads to build brand awareness. Spending an additional 400,000 might yield great results since there is a sizeable market which now knows of your product, and they are receiving targeted ads. But the relationship between ad spending and revenues might change again beyond 500k, because the market is saturated, or people are simply irritated with your ads. So, the linear relationship will have three phases or pieces, and should not be consolidated to one relationship alone. Now what is a poor data scientist to do when he or she is trying to predict the impact of ads on revenues? Use piecewise regression.
Piecewise Regression

Piecewise regression is a form of regression analysis in which the data is divided into distinct segments, and a separate linear regression model is fitted to each segment. This approach is useful when the relationship between the independent and dependent variables changes at certain points, known as breakpoints or knots.
Let us say the relationship between ad spend and revenue changes only once at a breakpoint where x (value of ad spend) = c (let us say, as in our example, USD 100,000. Then the piecewise regression formula will look like this:

Which means, we have:
The Individual Linear Models (or segmented linear models): such that each segment of the data has its own linear model, which means that the overall regression function is a combination of multiple linear functions.
Breakpoints/Knots: The points at which the data is divided into different segments. These breakpoints can be predefined based on domain knowledge or estimated from the data.
And potentially:
Flexibility: It can model non-linear relationships by fitting different linear relationships to different ranges of the data.
Continuity: Often, constraints are added to ensure that the regression lines meet at the breakpoints, ensuring the overall model is continuous.
What is new?
Now that we have learnt that we can create multiple linear regression models on our data to create a more powerful model, the question would be, “where are the breakpoints”? How do we decide where exactly the relationship between Y and X changes enough to require an additional linear regression line? While this can be done just by ‘looking’ at a scatter plot, there are more scientific ways to do it as well.
For this we go to Muggeo (2003), “Estimating Regression Models with Unknown Break-Points”, which is also the basis for the Python implementation of the most popular piecewise regression library. The justification of the paper clearly showcases why data scientists should be interested in the piecewise model and the related libraries, “In analysing such ‘kink-relationships’, one is usually interested in the break-point location and in the relevant regression parameters (that is, slopes of straight lines). The classical methods used to consider non-linear effects, such as polynomial regression, regression splines and non-parametric smoothing, are not suitable because the change-points are fixed a priori (regression splines) or are not considered at all (smoothing splines and polynomial regression). Furthermore, regression parameters obtained in regression splines or polynomial regression approach are not directly interpretable [12]. Thus, to estimate the model and to get meaningful parameters, alternative procedures have to be employed. In biomedical applications it is easy to see the effect of some risk factor on the response to change before and after some threshold value. For instance, in mortality studies, the relationship death–temperature is V-shaped, so it may be of interest to estimate the optimal temperature where the mortality reaches its minimum”.
Without going into the math (which is quite accessible and available in the paper), in short Muggeo (2023) uses a maximum likelihood estimator (which most data scientists would have seen when using logistic regression) to estimate α as the linear parameter for the first segment and β as the difference-in-slopes parameter (which means, α+β is the parameter for the second segment), and the key to fitting the segmented regression is to estimate the breakpoint (via linearization) where the Taylor series approximation will hold exactly. With MLE these three (α, β and the breakpoint) can be easily calculated through the process of iteration.
Example
The dataset has revenue-ad spend pair for 2000 stores. Unless you have it installed, we initially install piecewise-regression. There is another useful package (pwlf) which can be used instead with minor tweaks to the code.
# Fit a piecewise regression model
xx = market_data_large['Ad_Spending']
yy = market_data_large['Revenue']
x = xx.to_numpy(dtype=None, copy=False)
y = yy.to_numpy(dtype=None, copy=False)
pw_fit = piecewise_regression.Fit(x, y, n_breakpoints=1, n_boot=100)
In the above code block we fit the piecewise regression. Please note that we convert the Xs and the Ys to numpy arrays (since our data comes from a pandas dataframe). We specify in this case that the number of breakpoints is 1 but we will test later to check if this assumption is correct. We also specify the bootstrapping option, to ensure that the model does not converge to some local breakpoint and not search for more. We see in the diagram below that above the USD 1000 mark, the impact of ad spend on revenue actually increases which a linear regression model would not have been able to detect. If this pattern reverses again, we might get multiple breakpoints in our data.
To test for the optimal breakpoints, we use the model selection part of the library:
ms = piecewise_regression.ModelSelection(x, y, max_breakpoints=6)
The output of this line of code provides us with the BIC (and the minimum BIC provides the optimal breakpoints). For our data, the regression converges with 0, 1 and 2 breakpoints but the optimal is 1.
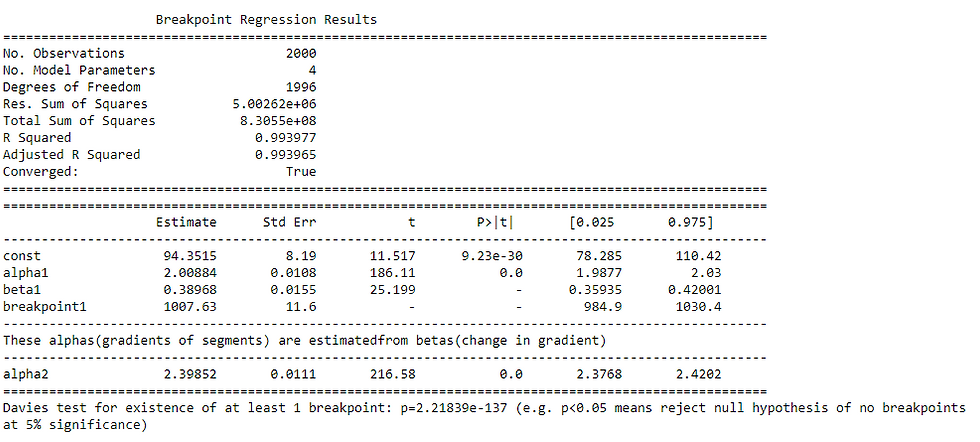
Now let us quickly look at the summary to interpret the values of importance:
The Davies test tells us that the p value is significantly lower than 0.05 implying the existence of a valid breakpoint. The estimated breakpoint is at the value 1007 (which is extremely close to our noise-added but simulated actual breakpoint of 1000). Alpha1 is the gradient which is roughly 2 for below the breakpoint and 2.4 above the breakpoint, showcasing a clear change in the impact of ad spend on revenue above and below the USD 1007 value. It seems that the impact of ad spend increases after the USD 1007 mark – probably an impact of minimum brand recognition.






Comments